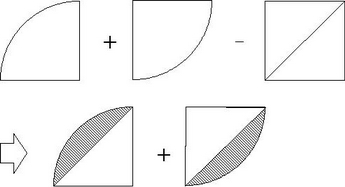
平面図形の面積の求め方(基本編) 円と正方形で覚えるルールはこの2つ! おうぎ形の面 中学受験に塾なしで挑戦するブログ―やってみてる編 塾に通わずに中学受験はできるの 上記の図で仮に円の半径が3cmであれば、正方形の面積は、 3×3×2=18 18cm2 となります。 右側の四分円の面積は 5×5×314×1/4= と求めることができる。 ちなみにこのレベルの学校を受けるなら5×5×314の答えが785だということは暗記しておこう。 四分円の面積が求められたので次は三角形dbfの面積を求める。

神戸女学院中2018年 面積ー 中学受験算数の良問 難問 基本問題
中学受験 面積 円
中学受験 面積 円-中学受験 5年 unit 5 いろいろな文章題1 集合・和と差 つるかめ算・つるかめカブトムシ算 差集め算 過不足算・平均 中学受験 5年 unit 6 円の面積 /11/5 エクタス算数科 中学受験の算数を勉強している生徒ならば、円の面積の求め方を知らない人は少ないと思われます。 円の面積の出し方は「半径×半径×円周率」と答える人がほとんどでしょう。 でも、円周率って何ですか? と聞かれる




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
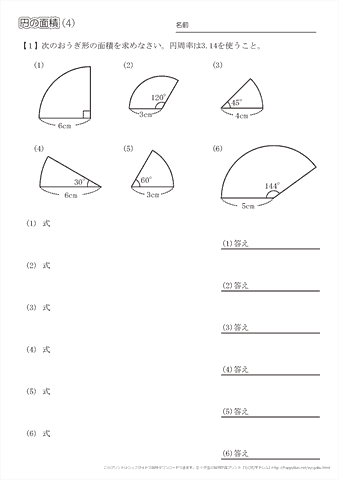
全般 内容 適度な難易度の面積の問題を90問集めました。 1ページ3問ずつで,式や筆算を書き込むスペースが十分あるので大変学習しやすくなっています。 また,解答解説はこれ以上ありえない位くわしく書いてあります。 面積の問題のPDFはこちら↓↓ 面積の問題 面積の問題解答・解説 面積の問題 割合で求める 円周率が314の時、下の図の アとイの面積比は1:057 となる。 上の考え方を使うと下の正方形と色のついた部分の面積比も 1:057 になる。 100:面積=1:057 面積=57㎠ と求めることができる。 円周率が314の時しか使えません。 公式として覚えているだけでは、中学生になってから問題を解けなくなってしまいます。 基本的な考え方で求められる円の面積公式を見直してみる 半径 × 半径 × 314 ですが、その半径が図のどの位置になるかを視覚的に確認してみます。 赤線や緑線が半径ですが、正方形の「A」とおうぎ形の「半径」は同じ長さです。
』) Amazon(アマゾン) 766〜4,723円 1 2つの円が交わってできる角 → 円の中心と結ぶ補助線 で、正三角形・二等辺三角形を発見 2難易度:★★★★☆☆中学入試難関校レベル 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 半径5cmの円と長方形ABCDを図のように重ねました。色のついた部分の面積の和は何今年の1問 21年 算数星人/カワタケイタ 浦和明の星女子中−円と正方形 21年;
平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式がまだ曖昧な人は こちらの記事 を読んでから、これから解説する問題に取り組んでください。 中学受験 算数21年 5年生 6年生 入試解説 円 埼玉 女子校 正方形 ★★★☆☆☆ (中学入試標準レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい



灘 開成 麻布 超難関校に挑戦 円周率 の引っかけ問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン



Q Tbn And9gcthgyy7mq2f9yeir5mtkl5mcopaxjhnujpgjn8admlcvveiesdw Usqp Cau
円とおうぎ形 円とおうぎ形 面積問題1 中学受験のための学習プリント http//manabihirobanet/ 2 答え ① ㎠ 別解2 ② が4個 ㎠ ③ ㎠ 2512 16 = 912 5 × 5 × 314 4 × 2 = 2512 4 × 4 = 16 4 × 4 × 314 ÷ 912 ÷ 4 5 × 5 456 456 × 2 = 912 4 = 1256 4 × 4 ÷ 2 = 8 4 × 4 × 314 ÷ ÷ 2 = 7125 例題 半径5cmの半円を、円Aを中心にして、45°回転させました。 黒くぬった部分の面積を求めなさい。おうぎ形の面積 を 求める力 が、理解できていれば、小学生が自分の力で、解答を導けるプリントを作りました♪パパママ向けのヒント解説も行っていますよ♪314×64=096 314×81= 正方形や円などの面積を速く正確に計算するために、同じ数をかけた積(二乗・自乗)の計算方法をマスターしましょう。 (参考) → 二乗の速算法 平面図形の面積の基本問題 問題1 次の図形の黒くぬった部分の面積を求めなさい。 → 解答




Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 への道



半円 算数星人のweb問題集 中学受験算数の問題に挑戦
中学受験 わからないので教えてください。よろしくお願いします。 下の図は、半径12cmの円の4ぶんの1の部分を3等分したものである。斜線部分の面積を求めなさい。ただし円周率 これが中学入試に出た図形問題! (15年、女子学院中学)円と求積 図のように直径10cmの円と、縦8、横6cmの長方形が2つあります。 影をつけた部分の面積は何c㎡ですか。 ただし、円周率は3.14とします。 図解と解法例はこちらに!中学受験算数はこちら タグ一覧 学校別に見る 文章問題はこちら 図形問題はこちら 計算問題はこちら 問題プリント 自動作成ツール みんなの算数オンライン



算数 面積と角度 中学受験 ベネッセ教育情報サイト



中学受験 算数 面積 よく出る応用問題や難問をわかりやすく解説 中学受験アンサー
中学受験算数問題(円の面積) 中学受験算数問題(ヒポクラテスの三日月) 中学受験算数(正方形の回転) 木の葉形の面積(1997 灘中 改題) 木の葉形面積(灘中1998 類題) 平面図形の面積(灘 07) 平面図形の面積 (三田学園 1998 改題) これが中学入試に出た図形問題! 解けるかな? 算数の難問に挑戦! 難問、奇問、名作にチャレンジ! 19年6月 3日 (月) ゲーム, 日記・コラム・つぶやき, 正方形, クイズ, パズル, 円, 算数, 中学入試, 相似, 木の葉形, 平面図形, 立体図形, 図形の移動, 正入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 直角二等辺三角形 立体の切断 ファイナル 21年 15年 図形の移動 共通部分 大阪 12年 13年 面積の和 ジュニア 展開図




中学受験算数 等積変形の利用 ヒポクラテスの月




半円を回転させる面積の問題 プリントを使って自分で解こう
円の面積=半径×半径×円周率(314) 中学受験では「基本」は"できて当然"というのが基本となって いるのが現実です・・・。ですので、確実にできるようにして おきましょう。 More from my site 算数「面積と角度」中学受験 中学受験 問題3 (久留米大学附設中 07年) <問題3の考え方と答え> = 314 − 2 = 114(cm²) でも、円の直径が正方形の対角線になっています。 このパターンはよく出てきますから、覚えておいてください。If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel



2015年 開成中学の面積問題から どう解く 中学受験算数




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル
中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合円と正方形(神戸女学院中学部 15年) 受験算数 , 平面図形 , 面積 上の図は、1辺12cm の正方形と 半径12cmの円一部を組み合わせたものから15テーマ。 鉄則とっても大事。 速ワザ算数平面図形編 (難関中学入試 ココで『差がつく! 算数「面積と角度」中学受験 図形について学習していきましょう。 取り上げるのは受験算数でも出題頻度(ひんど)の高い「面積と角度」です。 最初は難(むずか)しく感じるかもしれませんが、まずは基本的な問題で解き方・考え方をしっかり定着




長女の中学受験 算数の復習でできれば理解しておきたい図形問題 半径のわからないおうぎ形の面積 Pi Sukeのネットな生活




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
中学受験 算数プリントの主な内容 和差算 植木算 周期算 分配算 方陣算 展開図と見取図 等差数列のしくみ 円と多角形 割合の利用 百分率と歩合 消去算 代入算 円とおうぎ形 つるかめ算 平均の面積図 食塩水の問題 場合の数 ならべ方 数の性質 素因数分解とn進法 差集め算 旅人算 合同と相似 通過算 時計算 仕事算 ニュートン算 流水算 条件整理と推理の利用 立体と投影図 中学受験算数問題(円の面積)中学受験算数問題(ヒポクラテスの三日月)中学受験算数(正方形の回転)木の葉形の面積(1997 灘中 改題)木の葉形面積(灘中1998 類題)平面図形の面積(灘 07)正三角形と正六角形平面図形の面積 (三田学園 1998 改 元になる円の面積は314㎠ですので、その中心角60度分が答えですねd(^_^o) 道具④を使う問題例 その2 次の問題も図形の等積移動が伴う問題です。まずはパズル思考で考えてみましょう。




中学受験 円周率暗記プリント 体積問題で間違いを連発する2つの理由 かるび勉強部屋 中学受験 勉強 暗記
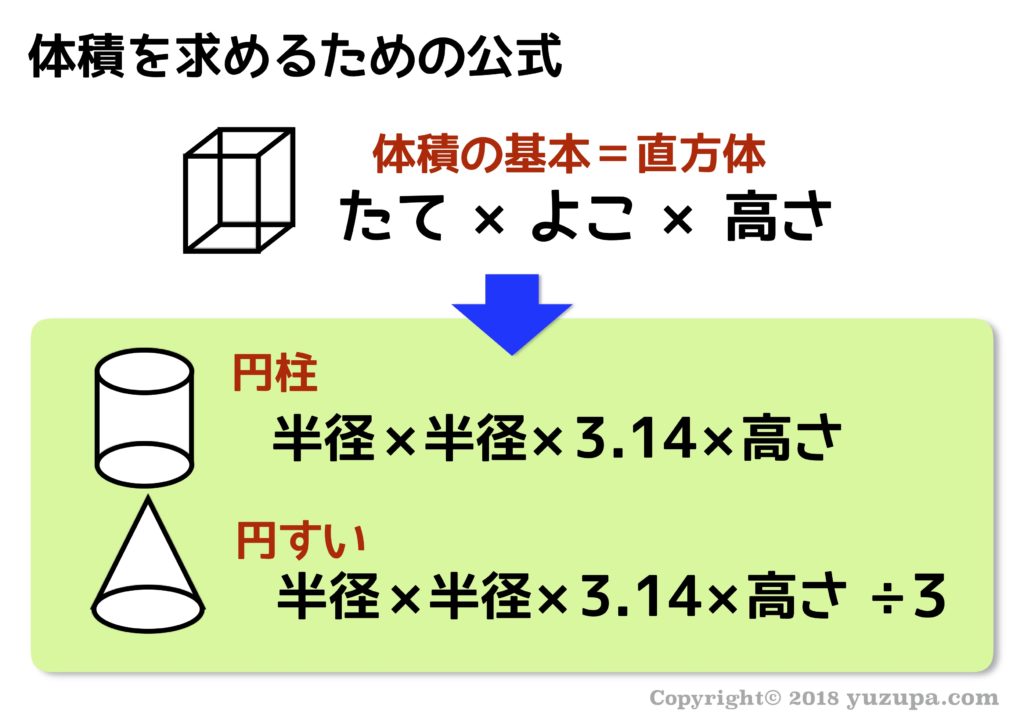



中学受験 円周率暗記プリント 体積問題で間違いを連発する2つの理由 かるび勉強部屋
第34問 内接円の面積比 図形ドリル 6年生 内接円 円 外接円 正三角形 正方形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアック 算数「面積と角度」中学受験 中学受験 問題5 図のように長方形の中に、各辺に接して半径5cmの2つの円が重なって入っています。 アの部分の面積がイの部分の面積の2倍と等しいとき、図のABの長さは何cmになるか答えなさい。 (西大和学園中・県外 08どう分ける? (中学受験算数 面積分割) どこに補助線を引いて、面積をどう分けるか? 三角定規を思い出すといいですね。 半径6cmの円があり、円周が12等分されています。 斜線部分の面積は何c㎡ですか。 ↓こんな風に分割できた? ヒント こたえ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



灘 開成 麻布 超難関校に挑戦 円周率 の引っかけ問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン
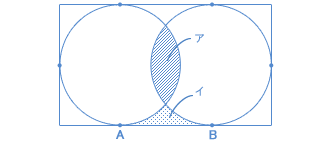
面積#6図形問題|算数円|灘中学校|中学受験|難問 面積#6図形問題|算数円|灘中学校|中学受験|難問 Watch later Share Copy「ウの円の面積=エの円の面積」です。 「ケーキの法則」を使うと、「イの面積=カの面積」もわかります。 また、 から、 ウが(2)の「イの斜線部分の面積の1/2倍~」の答えになることがわかりますので、 ウと等しいア、エ、クも(2)の答えとわかります。下の図の影の部分の面積を求めなさい。ただし、方眼の1目は2cm、円周率は314とします。 (東洋英和女学院中学部 年 問題3) 考え方 円と円が重なっている図形ですので、 「重なりは引く」 という解き方を用います。
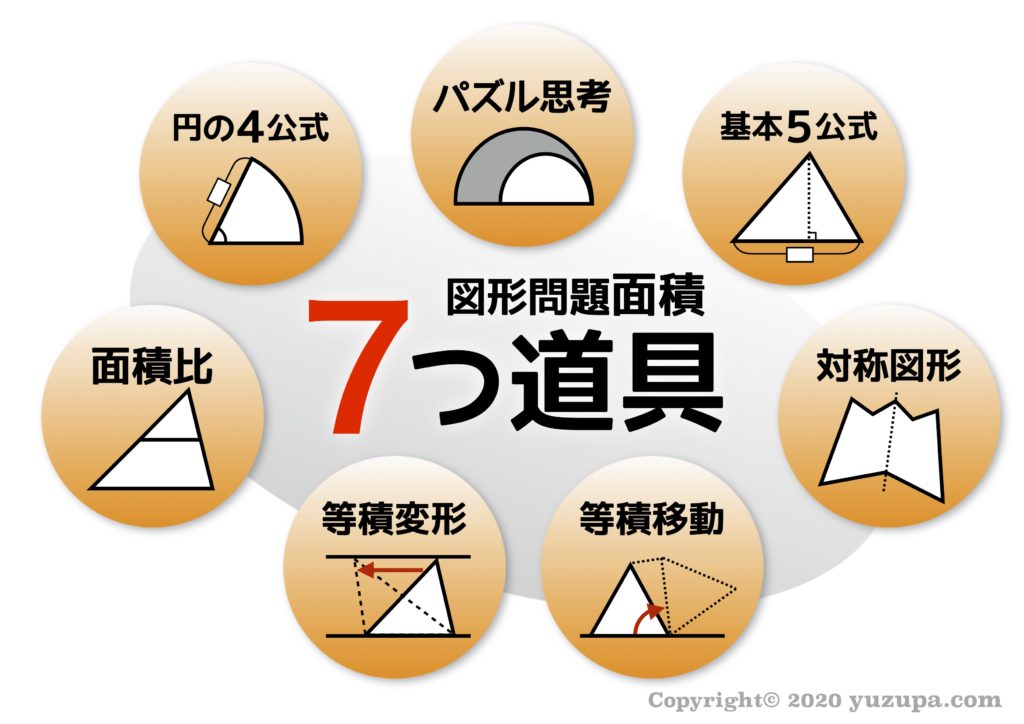



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



中学受験 算数 円の中の面積を求める 19年灘中入試問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト
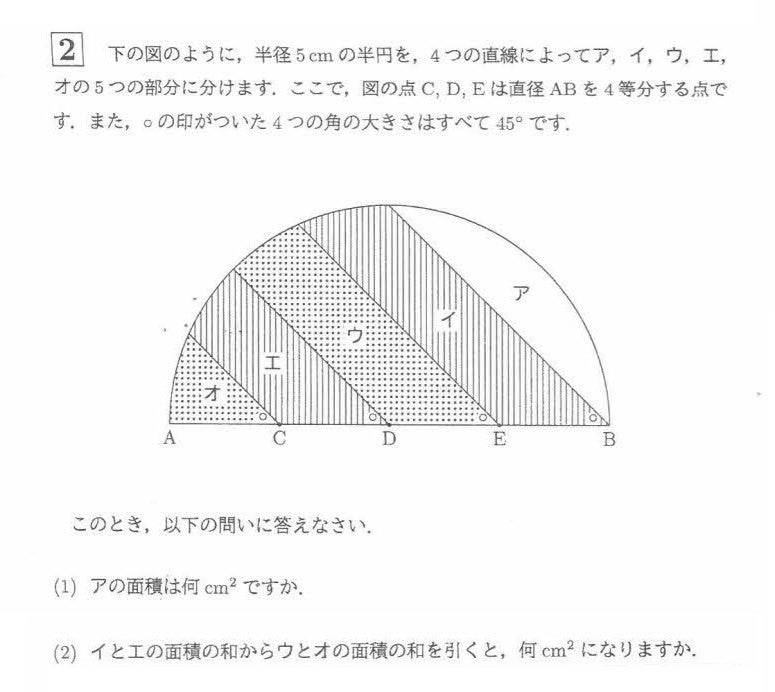



中学受験年度 面積の難問 東大カリスマ塾長 浜田一志公式ブログ 9割が伸びる 文武両道 勉強法




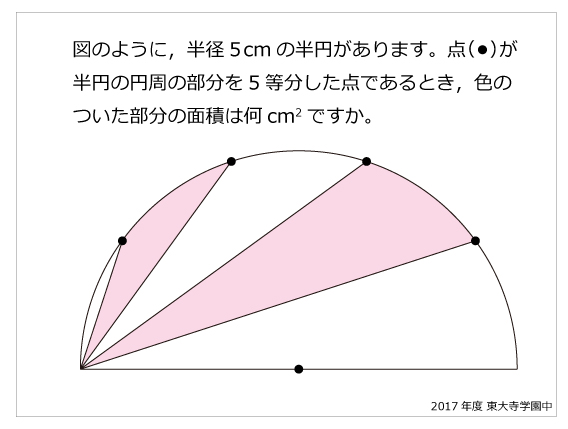
東大寺中2017年 平面図形ー 中学受験算数の良問 難問 基本問題
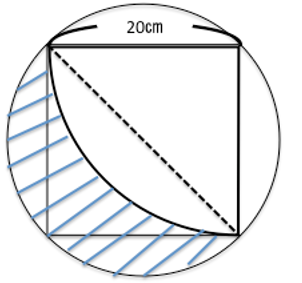



円の半径がでない問題の攻略法 中学受験プロ講師ブログ



中学受験 0 57 葉状図形求積数 学ぶ 楽しむ 世界を泳ぐ ができる数理の世界




平面図形の面積の求め方 基本編 中学受験 塾なし の
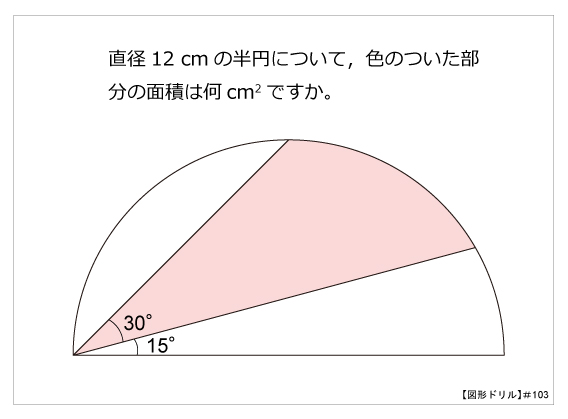



図形ドリル 第103問 半円の中の図形 算数星人のweb問題集 中学受験算数の問題に挑戦




大阪星光中2012年 面積ー 中学受験算数の良問 難問 基本問題




立命館中2019年 面積ー 中学受験算数の良問 難問 基本問題




円の面積
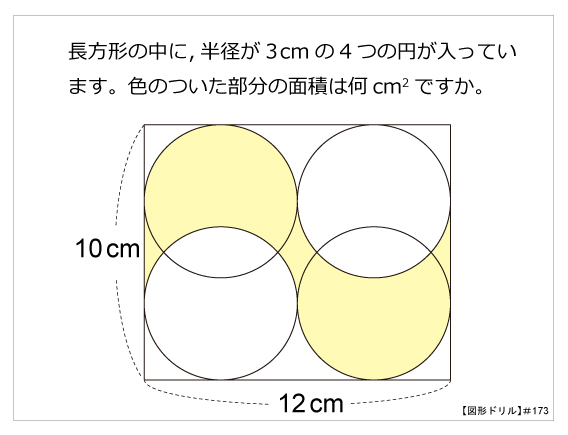



図形ドリル 第173問 複合図形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦
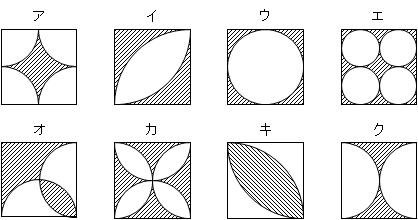



小5の学習ポイント2 円とおうぎ形 前田昌宏の中学受験が楽しくなる算数塾



1




浅野 円の面積を比べる ジーニアス 中学受験専門塾
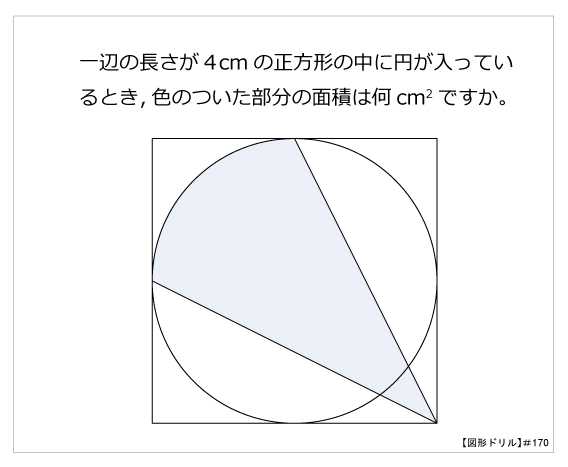



図形ドリル 第170問 円と正方形 算数星人のweb問題集 中学受験算数の問題に挑戦




面積比 難関私立中学受験問題 伊賀上野 はなまるせんせいの独り言



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル
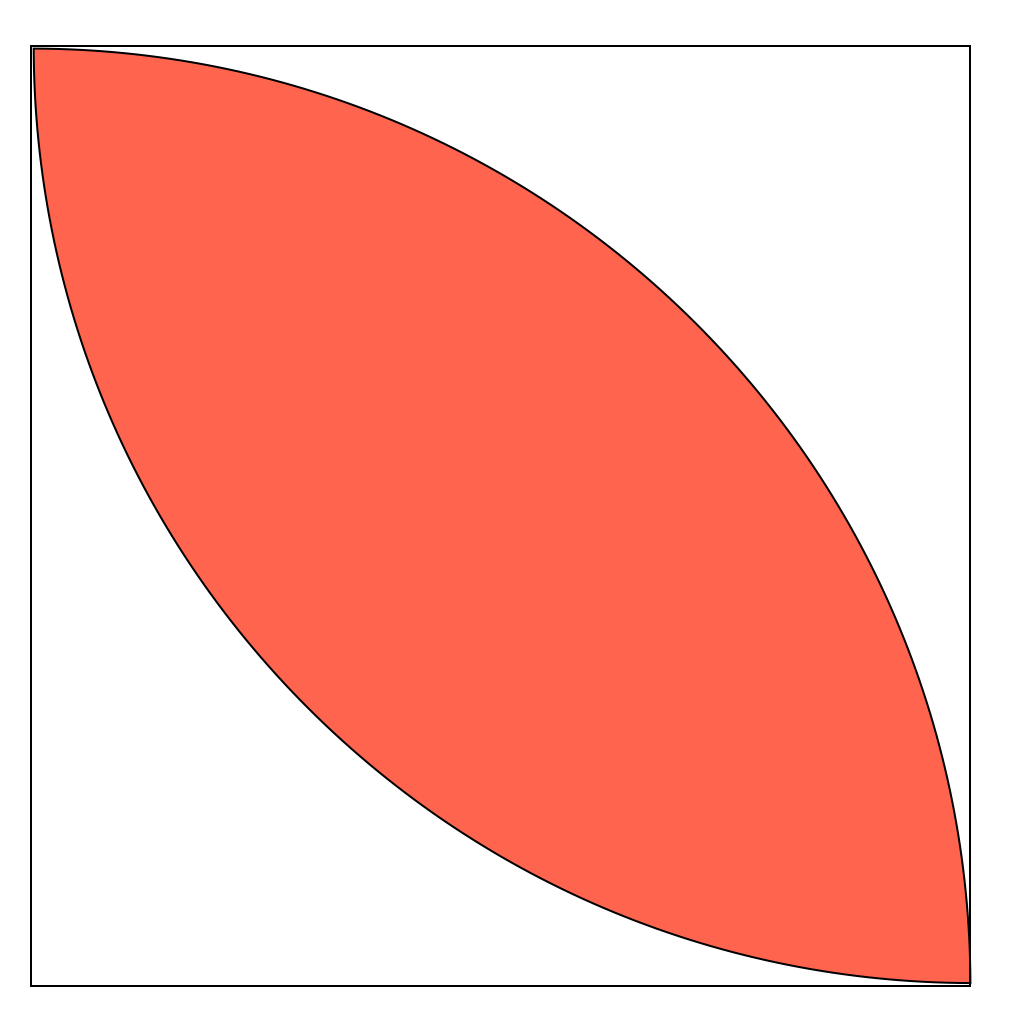



円とおうぎ形の面積 唇の形 カテキョウブログ




中学受験算数 等積変形の利用 ヒポクラテスの月



中学受験算数図形の問題です 長方形と4分円が重なっています アとイの面積が等し Yahoo 知恵袋




円の面積 練習応用 Youtube
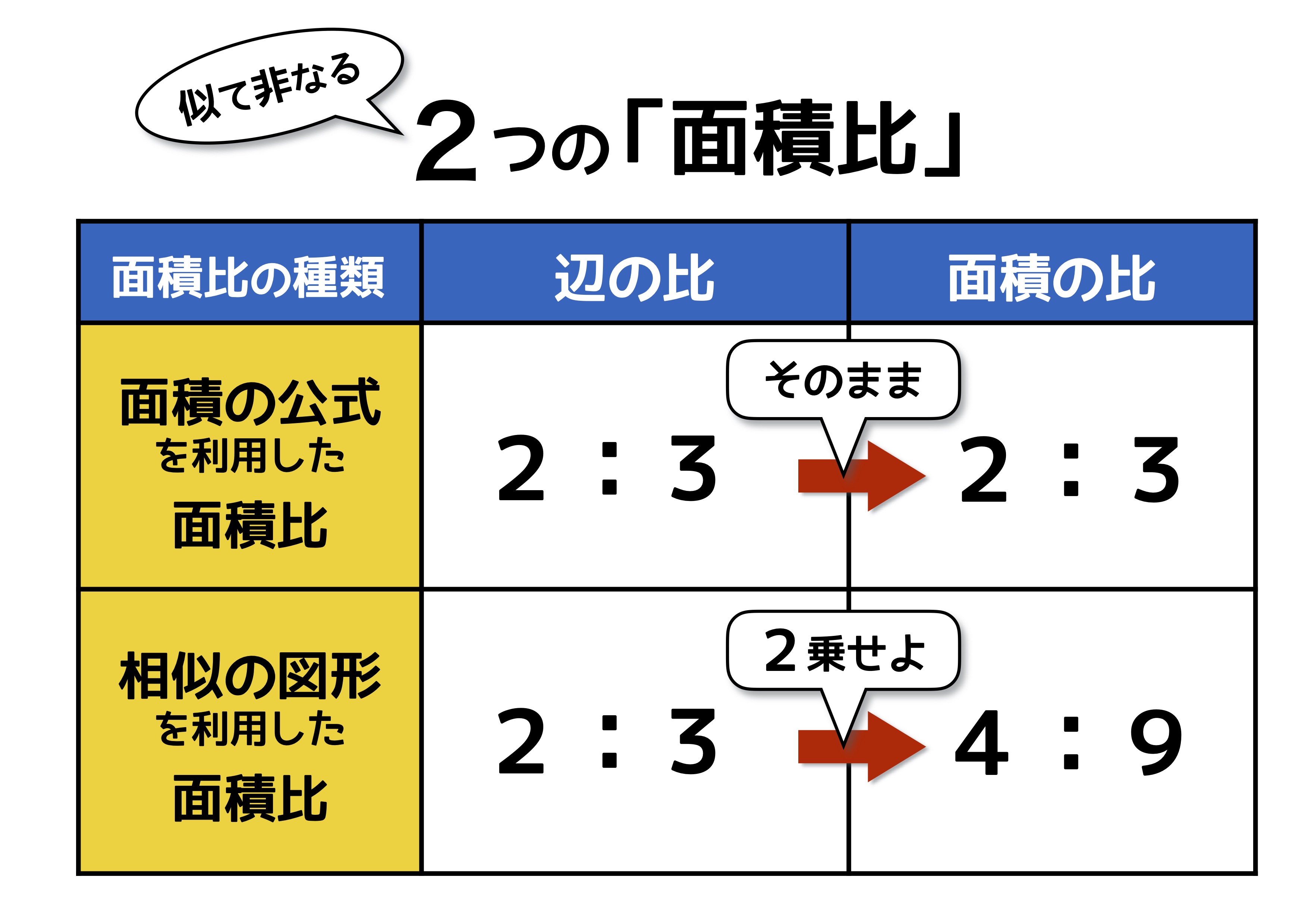



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
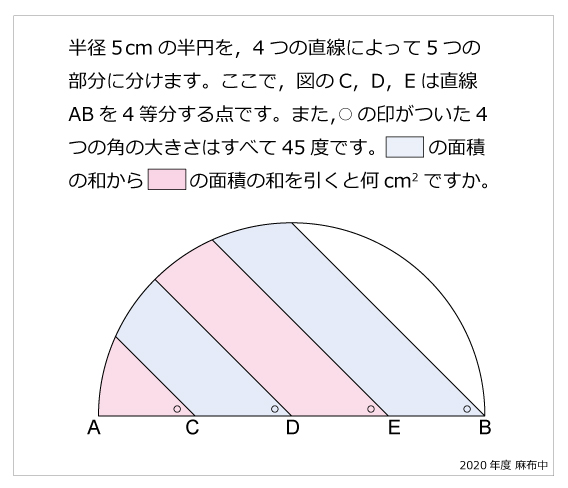



半円 算数星人のweb問題集 中学受験算数の問題に挑戦



3
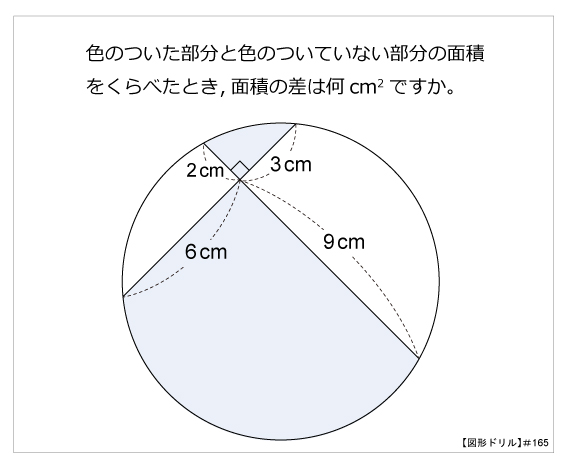



面積の差 算数星人のweb問題集 中学受験算数の問題に挑戦




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング




ヤフオク 算数 難関私立中学受験 高校受験対策に 革命的




中学受験 苦手な 図形 で得点力アップ 学習の秘訣は ポチたま中学受験
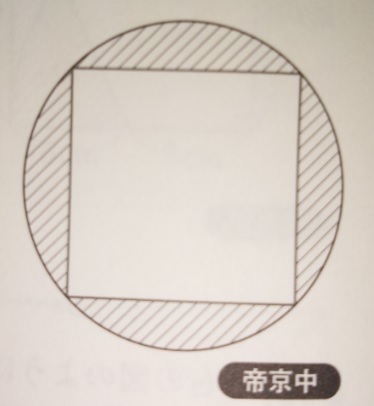



円と正方形で覚えるルールはこの2つ 中学受験 塾なし の勉強法
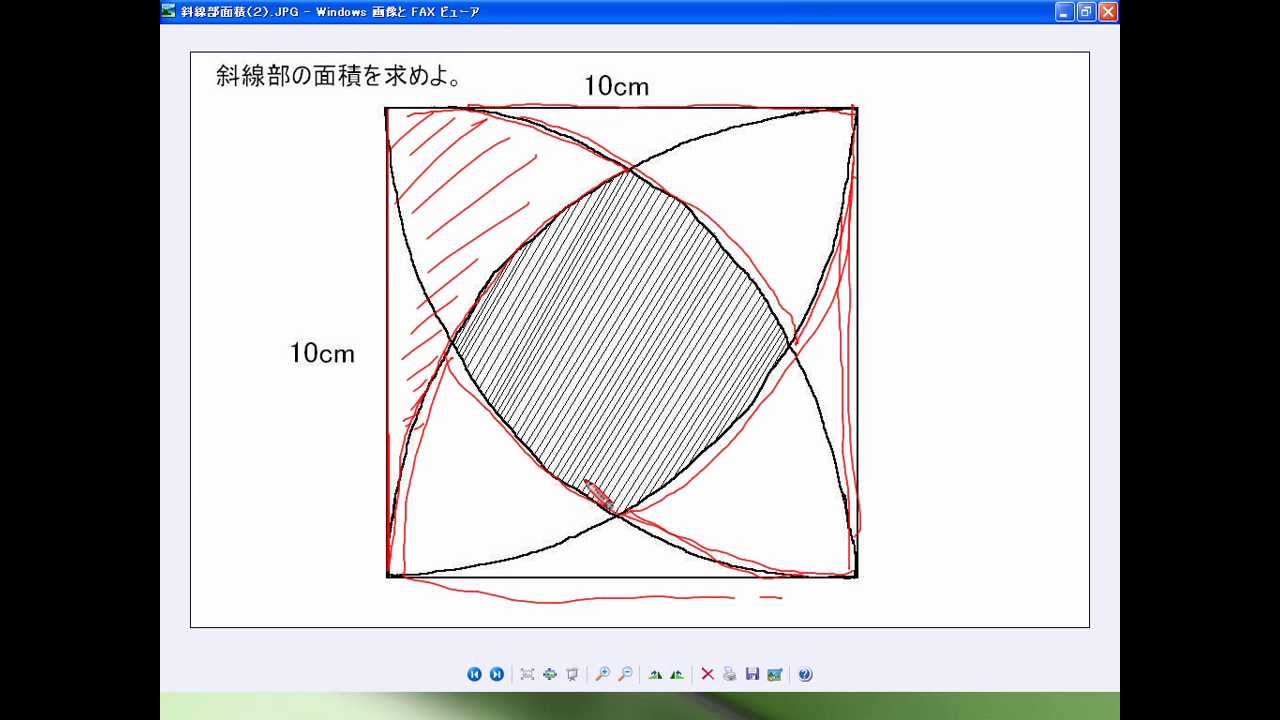



斜線部の面積 4 1辺10cmの正方形の場合 Youtube



0 57の暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾




面白い算数の問題 円 面積 算数 中学入試 Youtube




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング



1




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング



2




円の面積応用b 小学校 算数 中学 勉強 学習ノート



どう分ける 中学受験算数 面積分割 どう解く 中学受験算数




中学受験 クセモノ 動く点p 問題はパターンを知れば怖くない かるび勉強部屋



重なっている部分の面積はいくつ 中学受験算数 工夫する問 どう解く 中学受験算数



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



円 中学入試算数68分野別解法




算数苦手さん向けの 平面図形 円の面積 間違いポイントと対策 新小5 サピックス 中学受験 知識ゼロから合格へ




中附 半径の分からない円の面積 ジーニアス 中学受験専門塾




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




面積の求め方 算数の教え上手 学びの場 Com




山と数学 そして英語 小学校算数 円の面積に関する応用問題




灘中2019年 面積ー 中学受験算数の良問 難問 基本問題
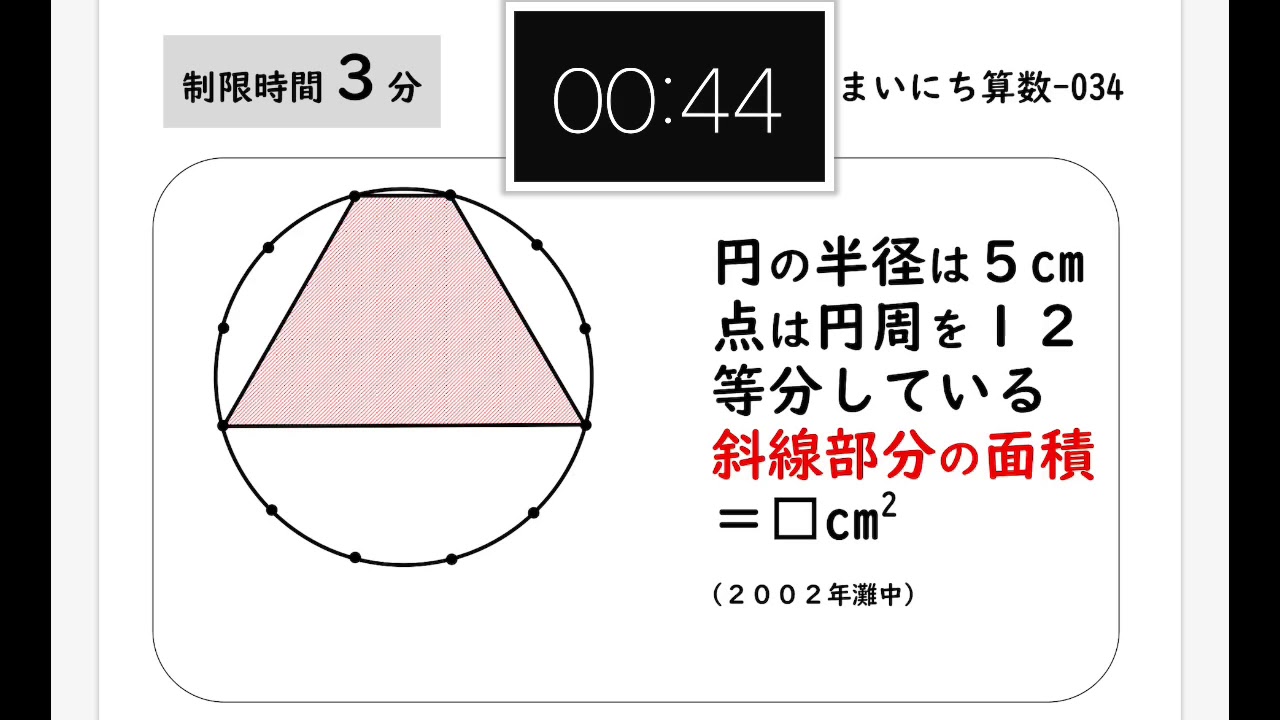



中学受験算数 まいにち算数034 多角形の面積 02年灘中 Youtube
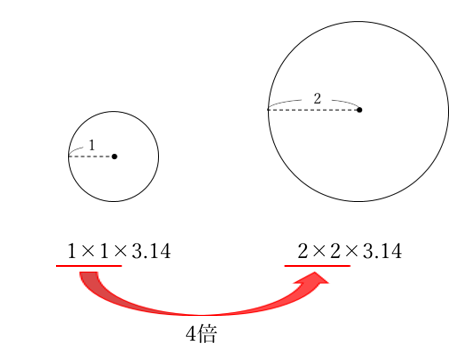



円の相似を利用した面積の計算 中学受験プロ講師ブログ




中学受験 円周率暗記プリント 体積問題で間違いを連発する2つの理由 かるび勉強部屋 中学受験 中学数学 暗記




無差別級算数 円の面積 受験算数に挑戦




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
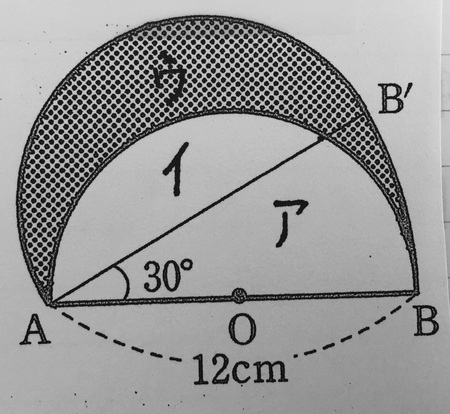



中学受験 高校受験 大学受験 興塾 正しい大人へ 先週 6 19 の解答 H27年度星陵中学入試問題



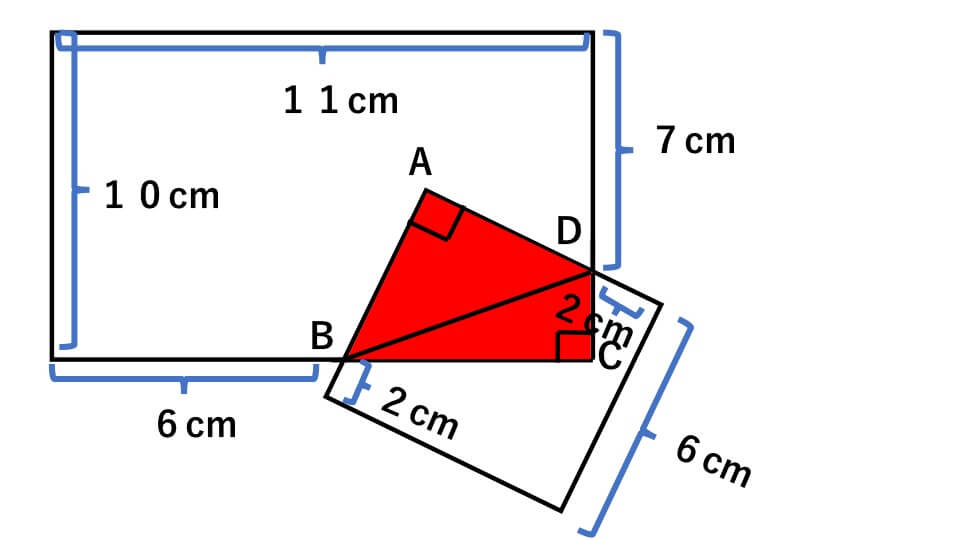
面積の計算です 中学受験の算数です 小学6年生の子供が複合図形の面積で下 Yahoo 知恵袋




半円を回転させる面積の問題 プリントを使って自分で解こう
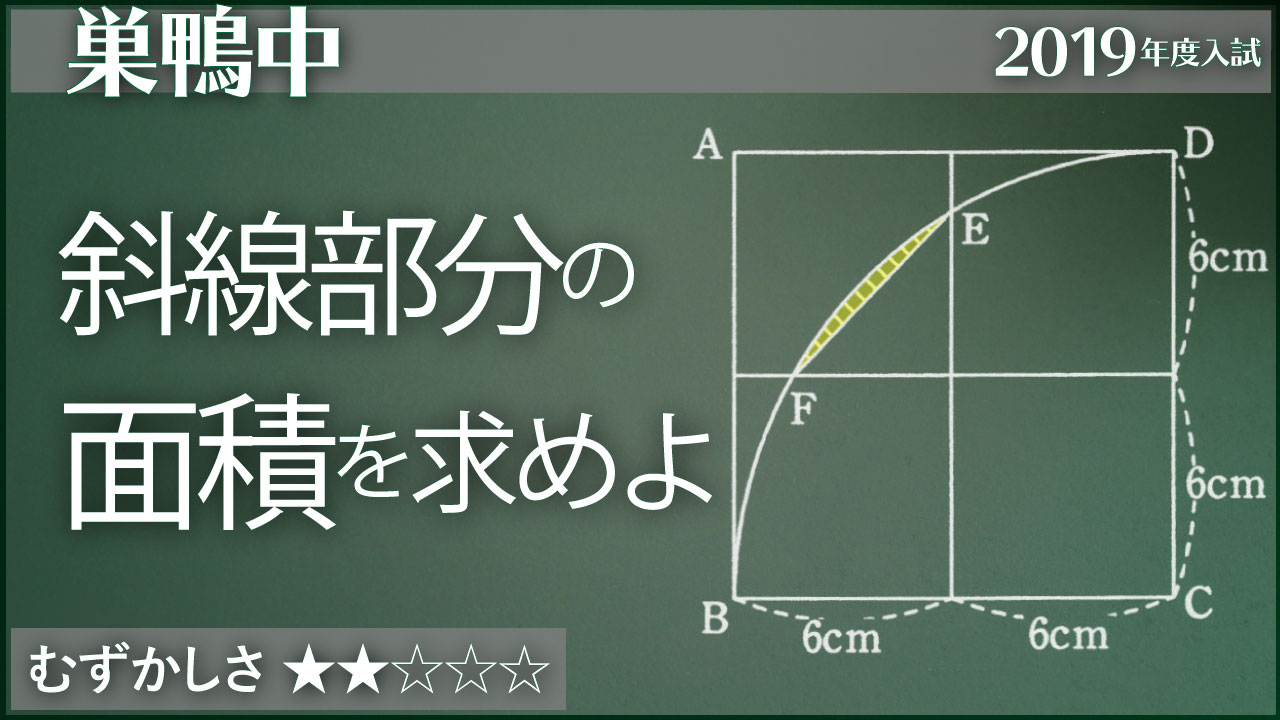



巣鴨 円の一部の面積を求める ジーニアス 中学受験専門塾




中学受験 算数 平面図形の面積 成り立ちから詳しく解説 中学受験アンサー




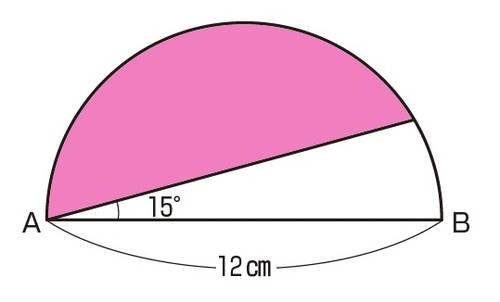
神戸女学院中2018年 面積ー 中学受験算数の良問 難問 基本問題



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋
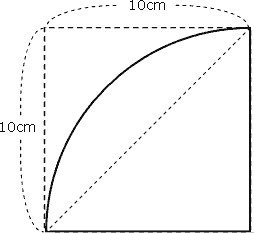



中学受験算数 円と面積 分配法則入門編 おまけ 中学受験情報部 Shiromaru Note



図は円の中に正方形が内接しているものですが このような円の面積 Yahoo 知恵袋



円 これが中学入試に出た図形問題
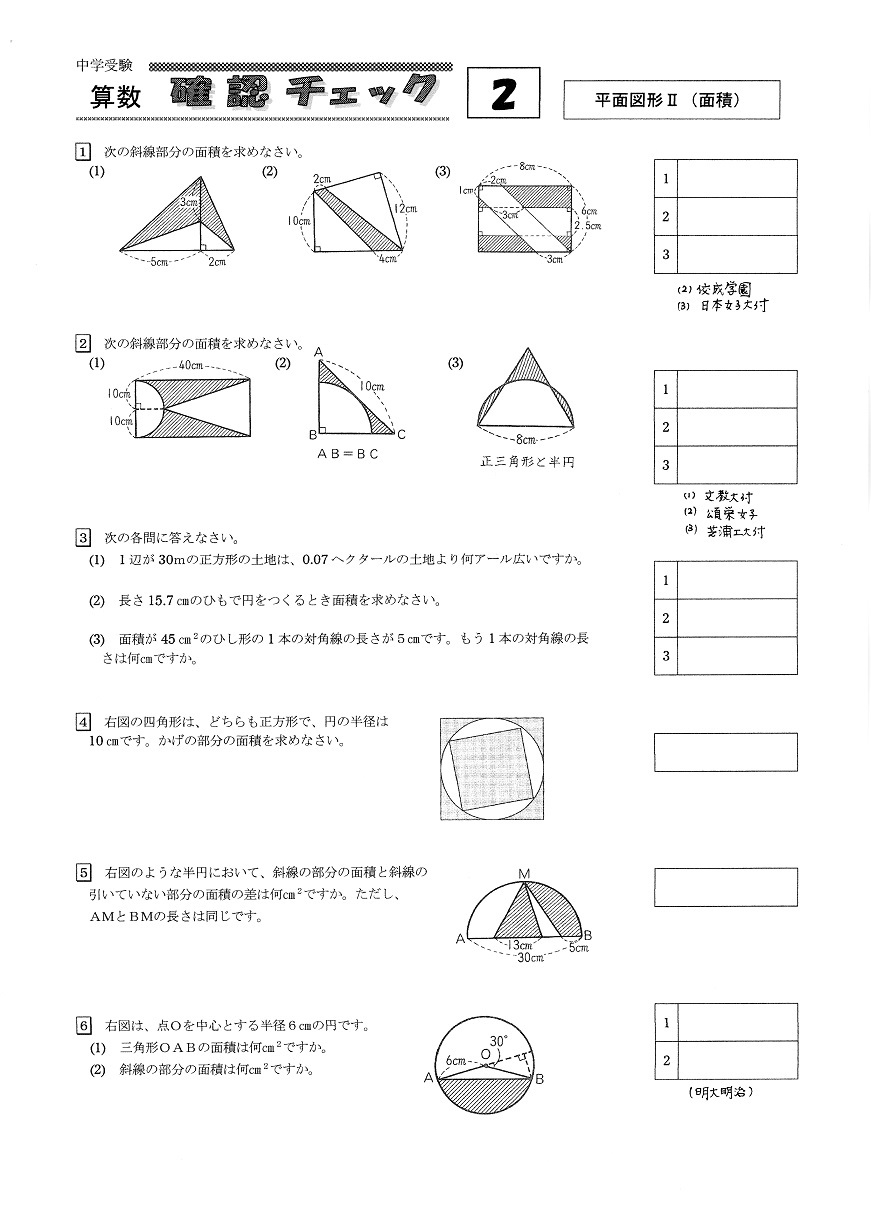



中学受験 算数確認チェック2 平面図形 面積 グランパは元塾長




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング




面白い数学問題 中学受験 中学入試 算数 解説 日本大学藤沢中学 平面図形 Youtube




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング




中学受験の算数 面積の問題 わからないので教えてください よろしくお願い Okwave



ヒポクラテスの三日月 これが中学入試に出た図形問題




算数苦手さん向けの 平面図形 円の面積 間違いポイントと対策 新小5 サピックス 中学受験 知識ゼロから合格へ
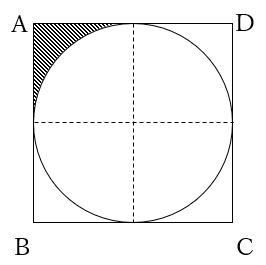



半径の分からない円の面積 中学受験プロ講師ブログ




算数図形編 面積 線分の長さ 対称な図形を追加してみよう 中学受験 高校受験パスナビ




15年度 愛光中学校 算数 1 6 面積




図形は共通部分に注目 知っている形 が見えてくる 海城中学校の入試から 親子で挑戦 中学受験算数 朝日新聞edua



円と扇形 中学受験ー算数解き方ポータル




中学校入試問題 算数 解いてください 半径9cmの円 を4分の1 に Okwave
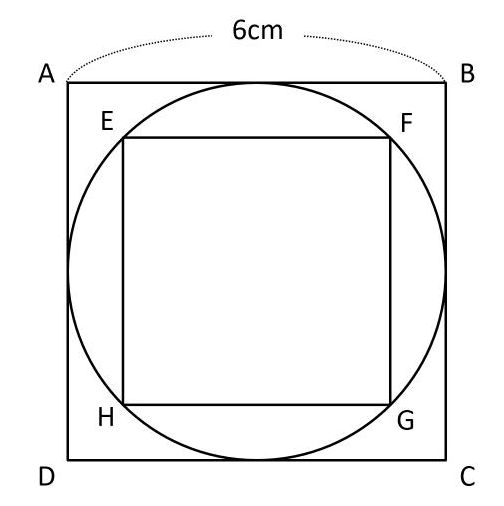



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ
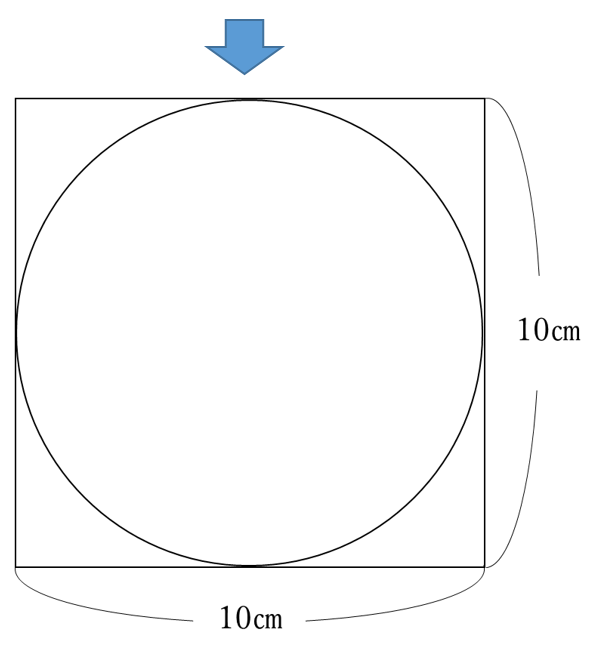



円の相似を利用した面積の計算 中学受験プロ講師ブログ




面積 6 図形問題 算数 円 灘中学校 中学受験 難問 Youtube




中学受験 算数 9月 円とおうぎ形 つるかめ算 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




15年度 愛光中学校 算数 1 6 面積
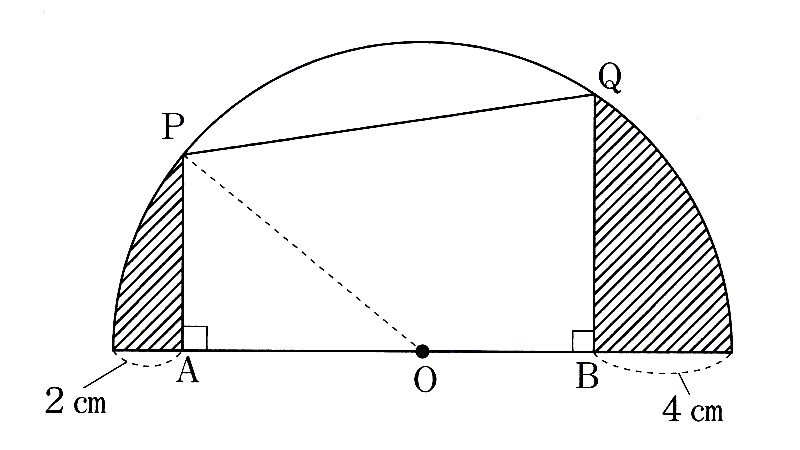



北辰塾 情報局 直撃 中学入試問題 第346回 大妻多摩 平面図形 おうぎ形と台形の面積
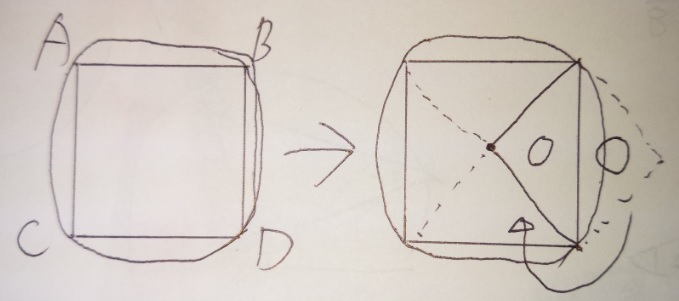



円と正方形で覚えるルールはこの2つ 中学受験 塾なし
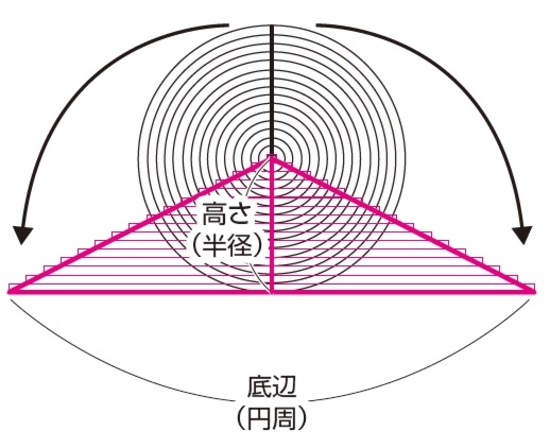



灘 開成 麻布 超難関校に挑戦 円周率 の引っかけ問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン


